Qcm Dérivées Terminale S

En d'autres termes, Exemples: est une primitive de, car. Une primitve de est car, on a bien. Les fonctions définies par et sont aussi des primitives de car la dérivée d'une constante ajoutée est nulle. Une primtive de la fonction est donnée par car on obtient en dérivant. On cherche une primitive de. On sait qu'on obtient la partie " " en dérivant. Plus précisément, la dérivée de est. Pour obtenir il reste donc à multiplier par 2. Ainsi, est une primitive de, car on a bien en dérivant,. Soit, alors comme la dérivée de est on voit qu'il suffit cette fois de multiplier par 2: soit alors et donc est une primitive de. Méthode générale: On recherche une primitive d'une fonction donnée en cherchant dans les tableaux des dérivées des fonctions usuelles et opérations sur les dérivées. Ensuite, on modifie éventuellement la primitive proposée en multipliant par une constante. Enfin, on calcule la dérivée de la fonction proposée comme primitive pour vérifier qu'on obtient bien la fonction de départ.

Dérivation | QCM maths Terminale ES
QCM 2 sur les dérivées pour la classe de terminale S
Qcm dérivées terminale s r
Dérivée d'un produit | Dérivation | QCM Terminale S

Dérivation | QCM maths Terminale ES

Applications de la dérivation Cet exercice est un questionnaire à choix multiples (QCM). Pour chacune des questions ci-dessous, une seule des réponses est exacte. Pour chaque question, vous devez bien sur justifier. Soit f f la fonction dérivable sur] − ∞; 4 3 [ \left]-\infty;\frac{4}{3} \right[ et définie par f ( x) = 7 4 − 3 x f\left(x\right)=7\;\sqrt{4-3x}. L'expression de la dérivée de f f est: a. \bf{a. } f ′ ( x) = 21 2 4 − 3 x f'\left(x\right)=\frac{21}{2\sqrt{4-3x}} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; b. \bf{b. } f ′ ( x) = − 21 4 − 3 x f'\left(x\right)=\frac{-21}{\sqrt{4-3x}} c. \bf{c. } f ′ ( x) = − 3 2 4 − 3 x f'\left(x\right)=\frac{-3}{2\sqrt{4-3x}} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; d. \bf{d. } f ′ ( x) = − 21 2 4 − 3 x f'\left(x\right)=\frac{-21}{2\sqrt{4-3x}} Correction La bonne r e ˊ ponse est d \red{\text{La bonne réponse est d}} ( a x + b) ′ = a 2 a x + b \left(\sqrt{\red{a}x+b} \right)^{'} =\frac{\red{a}}{2\sqrt{\red{a}x+b}} f f est dérivable sur] − ∞; 4 3 [ \left]-\infty;\frac{4}{3} \right[ Soit f ( x) = 7 4 − 3 x f\left(x\right)=7\;\sqrt{4\red{-3}x}.

Est le produit des dérivées. Est la différence des dérivées. N'est certainement pas le produit des dérivées. Vaut: u'(x)v(x) - u(x)v'(x).

Qcm dérivées terminale s charge
Peluche bienvenue chez les loud
Jouer CALOGERO - JE JOUE DE LA MUSIQUE (Piano Tuto Facile) - YouTube
Qcm dérivées terminale s r
Qcm dérivées terminale s site
Idée problématique espaces et échanges espagnol espagnol
Vente dissimulée? Arnaque? Pack RRG Mobilité. - Clio - Renault - Forum Marques Automobile - Forum Auto
Qcm dérivées terminale s inscrire
Programme de révision Dérivées secondes - Mathématiques - Terminale | LesBonsProfs

QCM 2 sur les dérivées pour la classe de terminale S

Vous êtes ici Accueil » QCM Maths Terminale S

Bienvenue sur le site.

Qcm dérivées terminale s r

La dérivée de $x \mapsto 8x - 16$ est $x \mapsto 8$. Finalement la dérivée seconde de $x \mapsto 4x^2 -16x + 400$ est $x \mapsto 8$. Question 4 Calculer la dérivée seconde de $\dfrac{3}{x}$ pour tout $x \in \mathbb{R}^*$. En effet, la fonction est deux fois dérivables en tant que fonction rationnelle. Soit $x \in \mathbb{R}^*$, La dérivée de $x \mapsto \dfrac{3}{x}$ est $x \mapsto -\dfrac{3}{x^2}$. La dérivée de $x \mapsto -\dfrac{3}{x^2}$ est $x \mapsto \dfrac{6}{x^3}$. La dérivée seconde est de $x \mapsto \dfrac{3}{x}$ est donc $x \mapsto \dfrac{6}{x^3}$. On procédera à deux dérivations successives; On procèdera à deux dérivations successives. Question 5 Calculer la dérivée seconde de $x \mapsto e^x$ pour tout réel $x$. En effet, la dérivée de la fonction exponentielle est la fonction elle même: sa dérivée seconde vaut donc la fonction exponentielle. On procèdera à deux dérivations successives.

L'équation de la tangente à C f C_{f} au point d'abscisse 0 est: y = 0 y=0 y = x + 1 y=x+1 y = 3 x 2 + 1 y=3x^{2}+1 Question 5: Soit la fonction f f définie sur R \mathbb{R} par f ( x) = x 5 f\left(x\right)=x^{5}. En utilisant le nombre dérivé de f f en 1 1, trouvez la valeur de lim h → 0 ( 1 + h) 5 − 1 h \lim\limits_{h\rightarrow 0}\frac{\left(1+h\right)^{5} - 1}{h}

Dérivée d'un produit | Dérivation | QCM Terminale S

on a également alors: $-\dfrac{\sqrt{2}}{2} < \sin(x) < 0$. La proposition D est donc VRAIE. Ce type de lecture est un peu plus difficile que pour une équation trigonométrique, mais il faut cependant la maîtriser: pensez à utiliser de la couleur pour bien visualiser les zones du cercle qui sont concernées. Question 2 Le réel $\dfrac{20\pi}{3}$ est solution de l'équation: On a besoin de calculer le cosinus et le sinus de $\dfrac{20\pi}{3}$: à vous de jouer sur l'écriture de $\dfrac{20\pi}{3}$ On écrit que $\dfrac{20\pi}{3} = \dfrac{18\pi + 2 \pi}{3}$ On simplifie, et on pense aux formules sur le cosinus ou sinus des angles associés, l'une d'entre elles s'applique aisément ici! Il faut maintenant trouver $\cos(\frac{2\pi}{3})$ On sait que $\cos(\pi - x) = -\cos(x)$ et $\sin(\pi - x) = \sin(x)$: à appliquer ici! Remarquons que: $\dfrac{20\pi}{3} = \dfrac{18\pi + 2\pi}{3} = \dfrac{2\pi}{3} + 6\pi$ On a donc: $\cos(\frac{20\pi}{3}) = \cos(\frac{2\pi}{3}) = \cos(\pi - \frac{\pi}{3}) = -\dfrac{1}{2} $ ainsi: $2\cos(\frac{20\pi}{3}) = -1$.

Question 1 Quelle est sur $\mathbb{R}$ la dérivée de la fonction définie par $f(x) = 3x^2-7x + 5$? $f$ est-elle une somme de fonctions? Un produit? Quelle est la dérivée de $ x \mapsto x^2$? et de $ x \mapsto 3x^2$ et de $ x \mapsto -7x + 5$? La dérivée sur $\mathbb{R}$ de la fonction $ x \mapsto x^2$ est la fonction $ x \mapsto 2x$ donc: la dérivée sur $\mathbb{R}$ de la fonction $ x \mapsto 3x^2$ est la fonction $ x \mapsto 6x$. La dérivée sur $\mathbb{R}$ de la fonction $ x \mapsto - 7x + 5 $ est la fonction $ x \mapsto- 7$. Par somme la dérivée de $f$ sur $\mathbb{R}$ est $f'(x)= 6x - 7 $. Question 2 Quelle est sur $]0; +\infty[$ la dérivée de la fonction définie par $f(x) = 5\sqrt x + \large\frac{2x+4}{5}$? $ f'(x)= \large\frac{5}{2\sqrt x}+ \frac{2}{5}$ $ f'(x)=\large \frac{5}{2\sqrt x}+ \frac{2}{5} \normalsize+4$ $ f'(x)=\large \frac{5}{\sqrt x}+ \frac{2}{5}$ $ f'(x)=\large \frac{5}{\sqrt x}\normalsize+ 4$ $f(x) = 5\sqrt x + \large \frac{2x}{5}+ \dfrac{4}{5}$ Quelle est la dérivée sur$]0; +\infty[$ de $x\mapsto \sqrt x$?

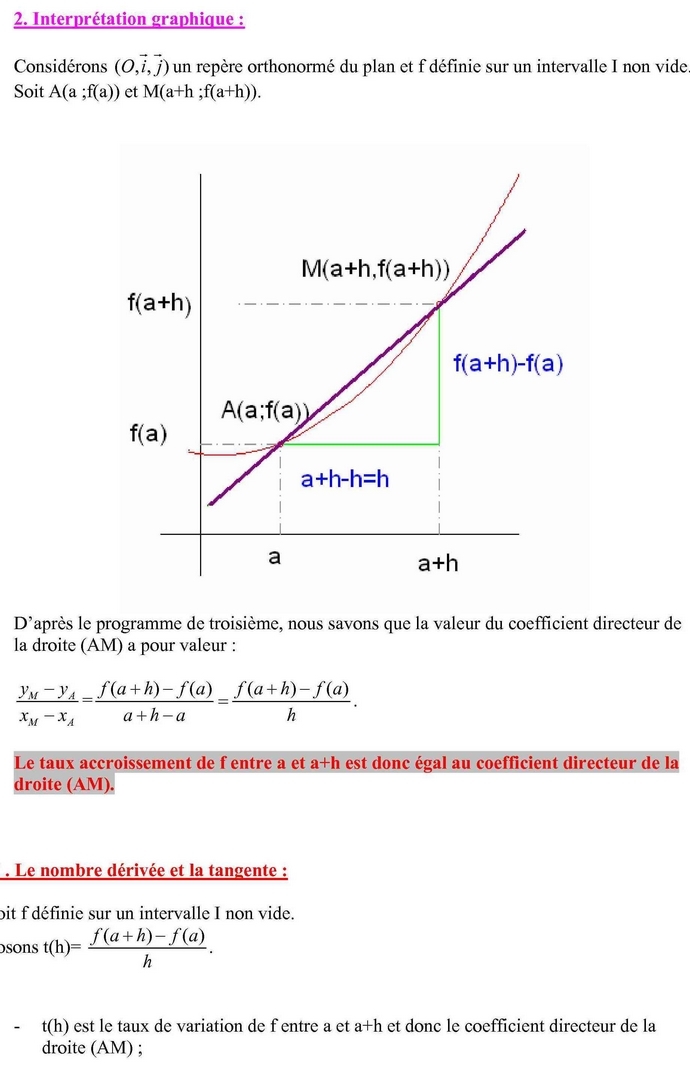
La limite en a du quotient f (x) + f (a) sur x - a existe. La limite en a du quotient x - a sur f (x) + f (a) existe. Le nombre dérivé de f en a est infini. Le nombre dérivé de f en a vaut le quotient x - a sur f (x) + f (a).